UP
[백준 11727 : PYTHON] 2xn 타일링 2 본문
문제 풀기 : 11727번
11726번: 2×n 타일링
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.
www.acmicpc.net
문제
2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.
아래 그림은 2×17 직사각형을 채운 한가지 예이다.

문제풀이
다음은 n = 4 까지의 경우의 수를 따져본 것이다.

+추가) n = 2일때 2x1을 2개 이어붙인 부분과 1x2를 2개 이어붙인 부분은 같은 모양으로 n=2의 경우의 수는 3가지가 아니라 2가지가 맞습니다! 그림을 잘못 그렸습니다. 참고해주세요!!
n = 3 부터 보면 n = 2과 n = 1의 타일 모양이 그대로 들어있다. 그러나! n = 1의 타일은 앞의 모양만 다르고 2번씩 들어가는 것을 볼 수 있다.
n = 4에서도 n = 3와 n = 2의 타일 모양을 그대로 가지고 있지만 n = 2의 경우가 2번씩 들어가는 것을 알 수 있다.
해당 규칙을 파악한대로 점화식을 작성해보면
dp[i] = dp[i-1] + 2 * d[i-2]
이라는 결론을 낼 수 있다.
이 외에 좀 더 간략하게 점화식을 파악해보자면
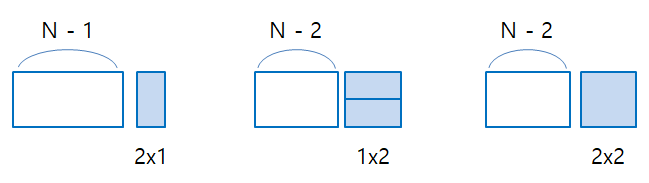
경우의 수는 이 세가지이므로 dp[i] = dp[i-1] + d[i-2] + d[i-2] = dp[i-1] + 2 * d[i-2]
이라는 결론에 빠르게 도달할 수 있다.
전체코드
import sys
input = sys.stdin.readline
n = int(input())
dp = [0] * 1001
# 초기값 지정
dp[0] = 1
dp[1] = 1
# 점화식에 따른 경우의 수 계산
for i in range(2, n+1):
dp[i] = dp[i-1] + 2 * dp[i-2]
print(dp[n]%10007)
반응형
'알고리즘 > DP' 카테고리의 다른 글
| [백준 1463 : PYTHON] 1로 만들기 (0) | 2021.03.10 |
|---|---|
| [백준 11726 : PYTHON] 2xn 타일링 (0) | 2021.03.10 |
| [백준 10844 : PYTHON] 쉬운 계단 수 (0) | 2021.03.10 |
| [백준 11057 : PYTHON] 오르막 수 (0) | 2021.03.10 |
| [백준 2193 : PYTHON] 이친수 (0) | 2021.03.10 |
Comments


